How To Find The Area Of A Rectangle With Perimeter

Perimeter and Area of Rectangle

The formula of perimeter and surface area of rectangle are explained step-by-step with solved examples.

If fifty denotes the length and b denotes the breadth of the rectangle, and so the

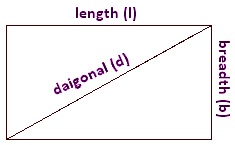
$Perimeter and Area of Rectangle$

● Perimeter of the rectangle = 2(50 + b) units

● Length of the rectangle = $\frac{P}{2}$ - b units

● Latitude of the rectangle = $\frac{P}{2}$ - 50 units

● Surface area of the rectangle = l × b sq. units.

● Length of the rectangle = $\frac{A}{b}$ units .

● Breadth of the rectangle = $\frac{A}{l}$ units

● Diagonal of the rectangle = $\sqrt{l^{2} + b^{two}}$ units

Let u.s.a. consider a rectangle of length 'a' units and latitude 'b' units.

$Perimeter of Rectangle$

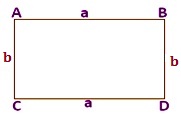
Therefore, perimeter of the rectangle ABCD

= (AB + BC + CD + DA) units

= (a + b + a + b) units

= (2a + 2b) units

= ii (a + b) units

Therefore,perimeter of the rectangle = two (length + latitude) units

We know that the area of the rectangle is given by

Area = length × breadth

A = a × b square units

⇒ a = $\frac{A}{b}$, i.east., length of the rectangle = $\frac{Area}{breadth}$

And b = $\frac{A}{a}$, i.e., breadth of the rectangle = $\frac{Surface area}{length}$

Worked-out problems on Perimeter and Area of Rectangle:

1. Find the perimeter and area of the rectangle of length 17 cm and breadth 13 cm.

Solution:

Given: length = 17 cm, breadth = 13 cm

Perimeter of rectangle = two (length + breadth)

= two (17 + 13) cm

= 2 × thirty cm

= 60 cm

Nosotros know that the area of rectangle = length × breadth

= (17 × 13) cm$^{2}$

ii. Find the latitude of the rectangular plot of land whose area is 660 m2 and whose length is 33 m. Find its perimeter.

Solution:

Nosotros know that the latitude of the rectangular plot = $\frac{Surface area}{length}$

= $\frac{660m^{2}}{33 chiliad}$

= 20 chiliad

Therefore, the perimeter of the rectangular plot = 2 (length + breadth)

= 2(33 + xx) thou

= 2 × 53 one thousand

= 106 m

iii. Find the area of the rectangle if its perimeter is 48 cm and its latitude is 6 cm.

Hither, P = 48 cm; b = vi cm

Therefore, 48 = 2 (l + 6)

⇒ $\frac{48}{2}$ = 50 + six

⇒ 24 = l + 6

⇒ 24 - 6 = l

⇒ 18 = l

Therefore, length = eighteen cm

Now, area of rectangle = 50 × b = 18 × 6 cm$^{2}$ = 108 cm$^{2}$

4. Find the breadth and perimeter of the rectangle if its area is 96 cm$^{2}$
and the length is 12 cm.

Solution:

Given, A = 96 cm$^{2}$ and l = 12 cm

A = l × b

Therefore, 96 = 12 × b

⇒ $\frac{96}{12}$ = b

⇒ b = 8 cm

At present, P = two (fifty + b)

= 2 (12 + viii)

= two × 20

five. The length and latitude of a rectangular courtyard is 75 m and 32 m. Find the cost of leveling it at the rate of $3 per m2. Also, find the distance covered by a boy to accept 4 rounds of the courtyard.

Solution:

Length of the courtyard = 75 m

Breadth of the courtyard = 32 m

Perimeter of the courtyard = 2 (75 + 32) m

= two × 107 m

= 214 m

Distance covered by the boy in taking 4 rounds = 4 × perimeter of courtyard

= iv × 214

= 856 m

We know that area of the courtyard = length × breadth

= 75 × 32 m$^{2}$

= 2400 thou$^{two}$

For 1 chiliad$^{two}$, the cost of levelling = $three

For 2400 m$^{2}$, the price of levelling = $3 × 2400

= $7200

Solved examples on Perimeter and Area of Rectangle:

half-dozen. A flooring of the room 8 yard long and six m wide is to exist covered past square tiles. If each foursquare tile is 0.8 thou, find the number of tiles required to cover the floor. Also, find the price of tiling at the rate of $7 per tile.

Solution:

Length of the room = eight one thousand

Breadth of the room = vi m

Surface area of the room = 8 × 6 k$^{two}$ {Expanse of room = Expanse of tiles that are put on the flooring of the room.}

= 48 m$^{2}$

Area of one square tile = 0.eight × 0.eight chiliad$^{2}$ = 0.64 1000$^{ii}$

Number of tiles required = $\frac{Expanse of floor}{Area of tiles}$

= $\frac{48}{0.64}$

= $\frac{48 × 100}{64}$

= 75 tiles

For 1 tile, the cost of tiling is $vii

For 7 tiles, the cost of tiling is $(vii × 75) = $525

7. The latitude of the rectangle is 8 cm and A its diagonal is 17 cm. Find the area of the rectangle and its perimeter.

Solution:

$Area of the Rectangle$

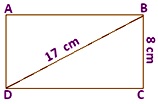
Using Pythagoras theorem,

BD $^{2}$ = DC $^{2}$ + BC $^{2}$

⇒ 172 = DC $^{ii}$ + 8 $^{2}$

⇒ 289 - 64 = DC $^{2}$

⇒ 225 = DC $^{two}$

⇒ 15 = DC

Therefore, length of rectangle = 15 cm

So, area of rectangle = 50 × b

= 15 × 8 cm $^{2}$

= 120 cm $^{2}$

As well, perimeter of rectangle = two (15 + 8) cm

= 2 × 23 cm

8. The length and breadth of the rectangle park are in the ratio 5 : 4 and its surface area is 2420 m2, find the cost of fencing the park at the rate of $10 per metre.

Solution:

Let the common ratio b 10,

then length of rectangular park = 5x

Latitude of rectangular park = 4x

Expanse of rectangular park = 5x × 4x

= 20x $^{2}$

According to the question,

20x $^{ii}$ = 2420

⇒ x $^{two}$ = $\frac{2420}{20}$

⇒ x $^{2}$ = 121

⇒ x = 11

Therefore, 5x = v × 11 = 55 and 4x = 4 × 11 = 44

And then, the perimeter of the rectangular park = two (50 + b)

= 2 (55 + 44)

= 2 × 99

= 198 cm

For i m, the cost of fencing = $10

For 198 one thousand, the cost of fencing = $198 × x

9. How many envelopes tin can be made out of a sail of newspaper 100 cm past 75 cm, supposing i envelope requires twenty cm by 5 cm slice of newspaper?

Solution:

Area of the sheet = 100 × 75 cm $^{2}$ = 7500 cm$^{two}$

Area of envelope = xx × v cm = 100 cm$^{two}$

Number of envelopes that can be made = $\frac{Area of canvas}{Expanse of envelope}$

= $\frac{7500}{100}$

10. A wire in the shape of rectangle of length 25 cm and breadth 17 cm is rebent to form a foursquare. What volition be the measure of each side?

Solution:

Perimeter of rectangle = 2 (25 + 17) cm

= two × 42

= 84 cm

Perimeter of foursquare of side x cm = 4x

Therefore, perimeter of rectangle = Perimeter of Foursquare

84 cm = 4x

⇒ 10 = 21

Therefore, each side of square = 21 cm

These are the detailed step-past-step explanation with the formula of perimeter and area of rectangle.

● Mensuration

Area and Perimeter

Perimeter and Area of Rectangle

Perimeter and Area of Square

Area of the Path

Area and Perimeter of the Triangle

Area and Perimeter of the Parallelogram

Area and Perimeter of Rhomb

Area of Trapezium

Circumference and Area of Circle

Units of Area Conversion

Exercise Test on Area and Perimeter of Rectangle

Practice Test on Area and Perimeter of Foursquare

●Mensuration - Worksheets

Worksheet on Area and Perimeter of Rectangles

Worksheet on Area and Perimeter of Squares

Worksheet on Area of the Path

Worksheet on Circumference and Surface area of Circle

Worksheet on Area and Perimeter of Triangle

Didn't detect what y'all were looking for? Or want to know more than data about Math Merely Math. Utilise this Google Search to find what y'all demand.